本文用分析学语言严格证明线性级、多项式级、指数级、阶乘级的大小关系。本文所说的大小关系均指各个数量级增长速率的大小关系。
首先用数学语言来描述各个数量级:![]()
- 线性级:
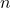
- 多项式级:
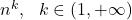
- 指数级:
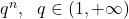
- 阶乘级:
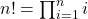
对于形如 ![]() 的式子,当
的式子,当 ![]() ,该式趋于0是显然的:
,该式趋于0是显然的:
(1) ![Rendered by QuickLaTeX.com \begin{equation*}\displaystyle \forall \epsilon>0, \exists N=\left[\left(\frac{C}{\epsilon}\right)^{\frac{1}{a}}\right], \forall n>N: \ \lvert \frac{C}{n^a}\rvert < \epsilon \end{equation*}](https://xhdeng19.com/wp-content/ql-cache/quicklatex.com-f7f3977f5f1941c785dc2f171f07ab59_l3.png)
1. 线性级和多项式级
由(1)式得
(2) ![]()
故线性级小于多项式级。
2. 多项式级和指数级
设![]() ,则
,则
(3) ![]()
由(1), (3)式和夹逼定理得
(4) ![]()
(5) ![]()
由(5)式得
(6) ![]()
故多项式级小于指数级。
3. 指数级和阶乘级
由(1)式和夹逼定理得
(7) 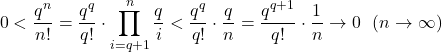
(8) ![]()
故指数级小于阶乘级。
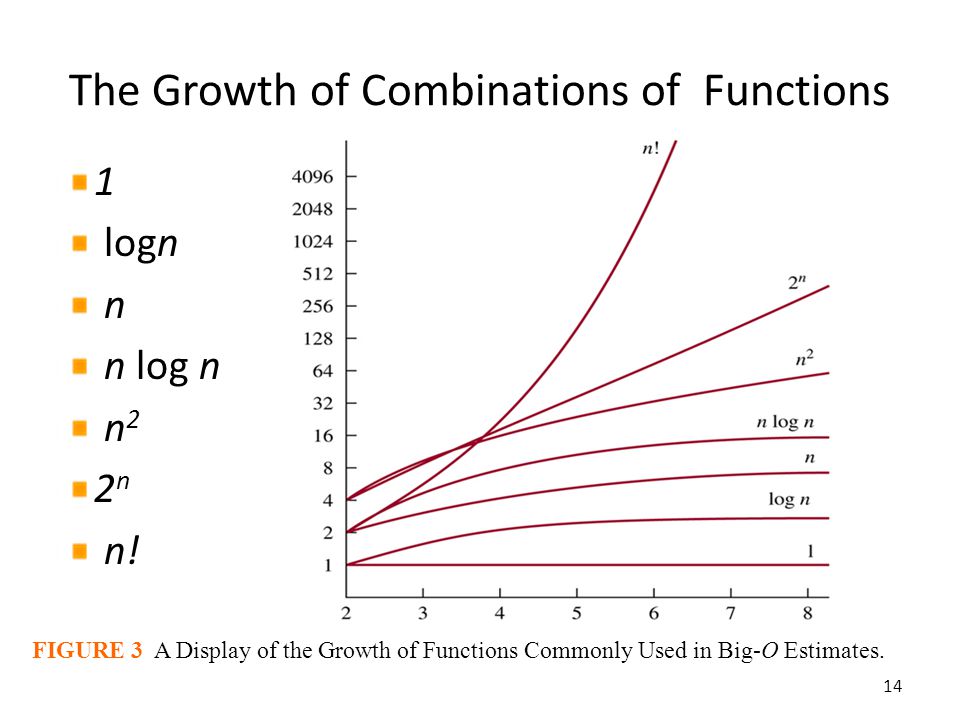
结语:综上,有大小关系:线性级<多项式级<指数级<阶乘级。

发表回复